公务员

排列组合公式：

；

数据比例关系：

某单位本科、研究生学历的职工人数之比为7：5，设方程人数分别为7x和5x

##工程问题：

工作总量=工作效率×工作时间

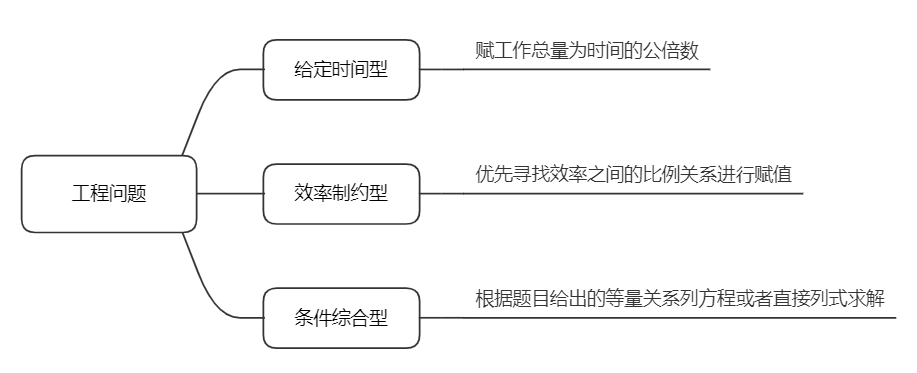
特值法：

1.合理利用特值,如设置效率比2:3,可直接设置每天做两个和做三个，求出特定的总量。

2.将甲，乙完成天数的最小公倍数设为工作总量

3.多个对象合作，且每个对象的工作效率一样时，设每个对象的工作效率为1

##最值问题：

和定最值问题需要;满足以下特征：

1、某几个量的和一定;

2、求其中某个量的最值。

和定最值的求解原则：

1、和一定时，当求某个量的最大值，让其他的量尽量小;

2、和一定时，当求某个量的最小值，让其他的量尽量大。

假设5个相异正整数的平均数是20，中位数是23，则此5个正整数中最大的数最大是多少?

其他情况：

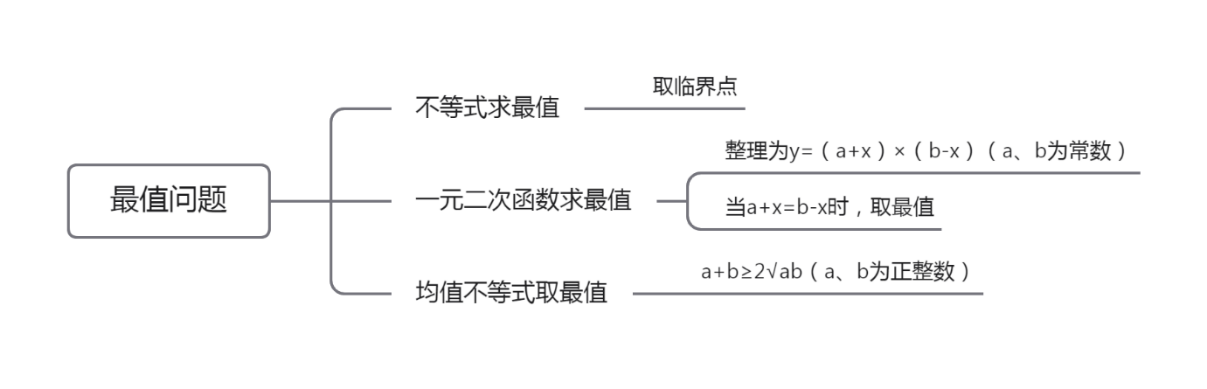
其中一元二次函数取极点，y有最值。

##年龄问题：

牢记年龄差不变

##和差倍比问题：

结合基本数量关系构造等量关系

除了题干中直接给出比例关系，分数、百分数也可转化为比例关系


`50%=1/2;

　　33.3%=1/3;2/3=66.7%

　　25%=1/4;3/4=75%

　　20%=1/5;2/5=40%;3/5=60%;4/5=80%

　　16.7%=1/6;5/6=83.3%

　　14.3%=1/7，2/7=28.6%

　　12.5%=1/8;3/8=37.5%;5/8=62.5%;7/8=87.5%

　　11.1%=1/9;2/9=22.2%;4/9=44.4%

　　10%=1/10;

　　9.1%=1/11;

　　8.3%=1/12;

　　7.7%=1/13;

　　7.1%=1/14;

　　6.7%=1/15;

　　6.25%=1/16;

　　5.9%=1/17;

　　5.6%=1/18;

　　5.3%=1/19;

　　5.0%=1/20

设未知数列方程求解:

某高校艺术学院分音乐系和美术系两个系别，已知学院男生人数占总人数的30%，且音乐系的男女生人数之比为1∶3，美术系男女生人数之比为2∶3。问音乐系和美术系的总人数之比为多少?

周期问题：

周期问题的两个关键是：

1.周期为T的数列，第n项=第n+aT项;

2.“几个周期”叠加在一起时，“总周期”是这几个周期的最小公倍数。

数列问题：

##行程问题：

##几何问题：

1.三角形的不等式性质：两边之和大于第三边，两边之差小于第三边，即a+b>c>a-b;

3.几何最值定理：

平面图形中，若周长一定，越接近于圆，面积越大;

平面图形中，若面积一定，越接近于圆，周长越小。

注：在平面图形中，最常考的是四边形：

即：若四边形周长一定，越接近于正四边形，面积越大;若四边形面积一定，越接近于正四边形，周长越小。

立体图形中，若表面积一定，越接近于球，体积越大;

立体图形中，若体积一定，越接近于球，表面积越小。

##容斥问题：

二者容斥、三者容斥和容斥极值

三者容斥就是研究三个集合间交叉关系的一类问题：

图中A、B、C分别表示三个集合，而M表示不属于三个集合的部分。此时我们不难发现，全集I就是由A、B、C以及M四个集合加和构成的，只是在加和的过程中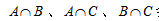，会被重复计算，因此需要将多算的这些减掉，在这过程中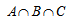，被连续减掉了三次，需要再把它加回来，由此可得三者容斥的核心公式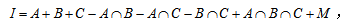公式看起来比较麻烦，但在实际应用中只需要直接代数即可。

三者容斥还存在第二种类型，它不具备如此明显的集合间交集的数据，它的表述通常为“同时属于两者的”、“三者都满足的”等方式，此时题目当中找不到有关于两两交集的数据，只能找到同时属于两个集合的数据的总和，因此就要求我们对于全集I重新划分，如图所示：

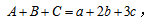其中1,2,3这三个部分只属于一个集合，我们就说他们分别只具备一种属性，用a来表示，4,5,6这三个部分同时属于两个集合，也就是分别具备两种属性，用b来表示，7这部分同时属于三个集合，即同时具备三种属性，用c来表示，而不属于任何一个集合的8则不具备任何属性，我们用d来表示。通过重新划分，我们发现，全集还可以由只具备一种属性的数据、同时具备两种属性的数据、具有三种属性的数据以及不具备任何属性的数据之和共同构成，所以又可以写成而集合A、B、C的加和又可以表述为两式联立就得到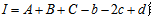：。通常这类题目的呈现方式如下：